POTENCIACIÓN Y RADICACIÓN (SUS PROPIEDADES)
Las potencias están formadas por la base y por el exponente. La base es el número que se está multiplicando varias veces y el exponente es el número de veces que se multiplica la base.
¿Qué es la base?
Es el número que se está multiplicando.
¿Qué es el exponente?
Las veces que se repite el número.
¿Cómo se forma una potencia?
Se disponen de la siguiente manera: el número de la base de escribe de forma normal, y el número de la potencia se escribe más pequeño que la base en la parte superior derecha.
Vamos a verlo con el siguiente ejemplo:
5 x 5 x 5 x 5 x 5 x 5 x 5
- ¿Qué número se está multiplicando? El 5, por lo tanto es la BASE
- ¿Cuántas veces se repite el número? 7 veces, por lo tanto es el EXPONENTE
Escribiendo la potencia quedaría así:

Vamos a ver otro ejemplo:
3 x 3 x 3 x 3
- ¿Qué número se está multiplicando? El 3, por lo tanto es la BASE
- ¿Cuántas veces se repite el número? El número se repite 4 veces, por lo tanto es el EXPONENTE
3 x 3 x 3 x 3 = 3 4
PROPIEDADES DE LA POTENCIA
Potencias con exponente 0
Son aquellas que tiene como base un número y como exponente el cero o elemento neutro y equivalen a la unidad.
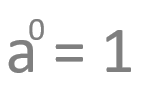
Vamos a ver un ejemplo: 2 elevado a 0 es igual a 1.
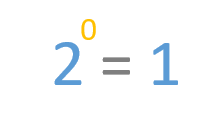
Potencias con exponente 1
Son aquellas que tiene como base un número y como exponente la unidad y son equivalentes a la base sin exponente. Sé que es algo muy evidente pero sigue siendo una peculiaridad de las potencias.
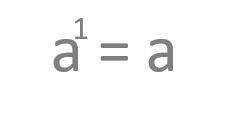
Vamos a ver un ejemplo: 2 elevado a 1 es igual a 2.
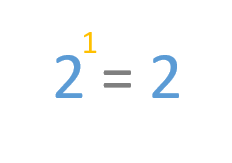
Producto de potencias con la misma base
En este caso, vamos a ver lo que ocurre cuando multiplicamos dos potencias que tienen la misma base (a) y, por contra, tienen exponentes diferentes (n y m). Esta expresión se puede simplificar con una potencia con la misma base y sumando ambos exponentes (n + m). 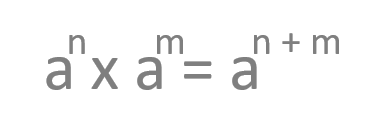
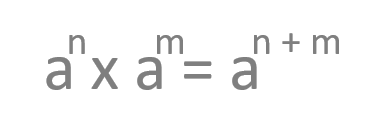
Vamos a ver un ejemplo: Multipliquemos 2 elevado a 2 por 2 elevado a 3 y veremos como es lo mismo que 2 elevado a 5.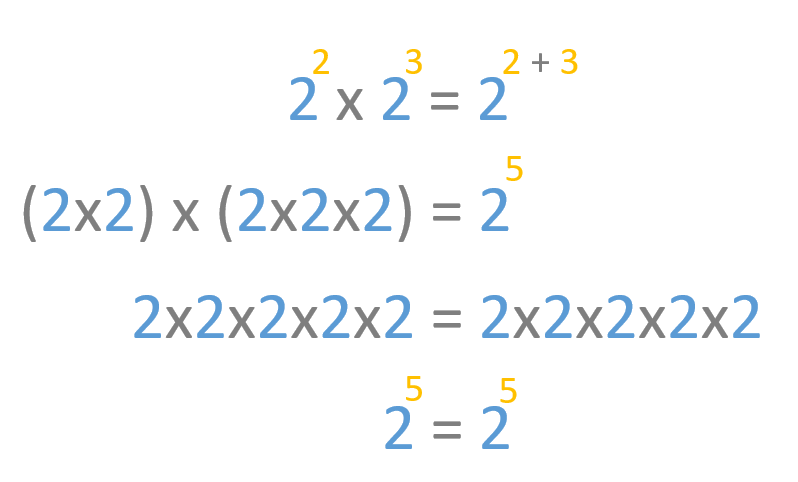
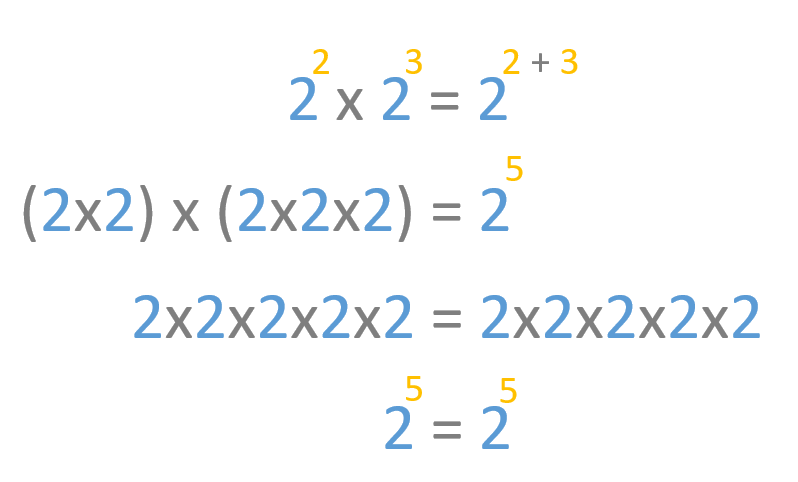
Producto de división con la misma base
En este caso, vamos a ver lo que ocurre cuando dividimos dos potencias que tienen la misma base (a) y, por contra, tienen exponentes diferentes (n y m). Esta expresión se puede simplificar con una potencia con la misma base y restando el exponente del dividendo al del divisor (n – m).
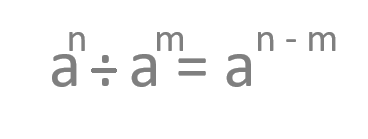
Vamos a ver un ejemplo: Dividamos 2 elevado a 4 entre 2 elevado a 2 y veremos como es lo mismo que 2 elevado a 2.
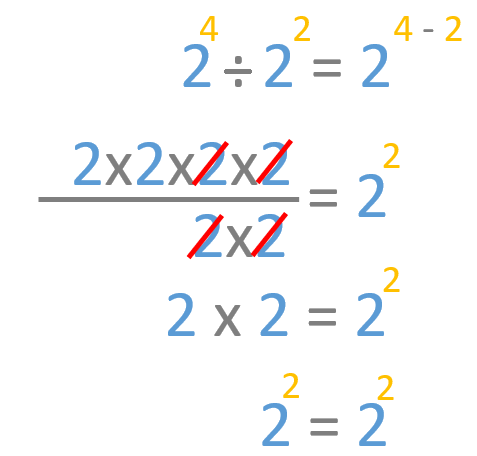
Espero que este post te sirva para comprender mejor cuales son y por qué son así estas propiedades de las potencias. Dejo para el siguiente post el resto de las propiedades. Mejor ir poco a poco.
Fuente: https://www.smartick.es/blog/matematicas/recursos-didacticos/potencias-que-son-y-para-que-sirven/
Actividad:

RADICACIÓN
La radicación se define como la operación inversa de la potenciación. La potenciación es una expresión matemática que incluye dos términos denominados: base a y exponente n. Se escribe de la siguiente forma:
Se lee como, “a elevado a n”
Para comprender mejor la definición de radicación, supongamos que nos dan un número a y nos piden calcular otro, de forma tal que, multiplicado por si mismo un número b de veces nos da el numero a. Por ejemplo si queremos averiguar qué número multiplicado por si mismo 2 veces da 196, obtenemos como resultado, 14.
Se llama raíz cuadrada de un número (algunas veces se abrevia como raíz a secas) a aquel otro que siendo mayor o igual que cero, elevado al cuadrado, es igual al primero. En la radicación El número que está dentro de la raíz se denomina radicando (a), el grado de una raíz se denomina índice del radical (n) el resultado se denomina coeficiente (k).
Las propiedades de la radicación son bastante parecidas a las propiedades de la potenciación, ya que una raíz es una potencia con exponente racional.
Ejemplo de un radical en forma de potencia:
Veremos ahora las propiedades de la radicación:
• Es distributiva con respecto a la multiplicación y a la división.
Veamos un ejemplo:
En la división,
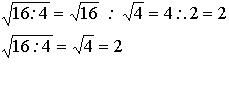
En la multiplicación,
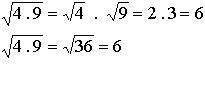
• No es distributiva con respecto a la suma y a la resta.
Ejemplos:
Ejemplos:
En la suma,
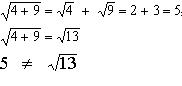
En la resta
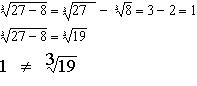
• Si el índice es par entonces el radicado tiene que ser positivo y la raíz entonces dos resultados, uno positivo y otro negativo, para este nivel utilizamos el resultado positivo.
Ejemplos,
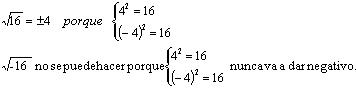
Si el índice es impar entonces la raíz va a tener el mismo signo que el radicando,
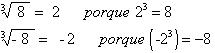
Si tengo una raíz de raíz se multiplican los índices.
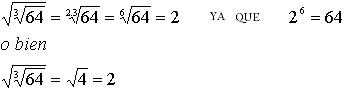
| |||||||||||||||||
Hola 😛
ResponderBorrar