RECTA NÚMERICA Y PLANO CARTESIANO
RECTA NÚMERICA
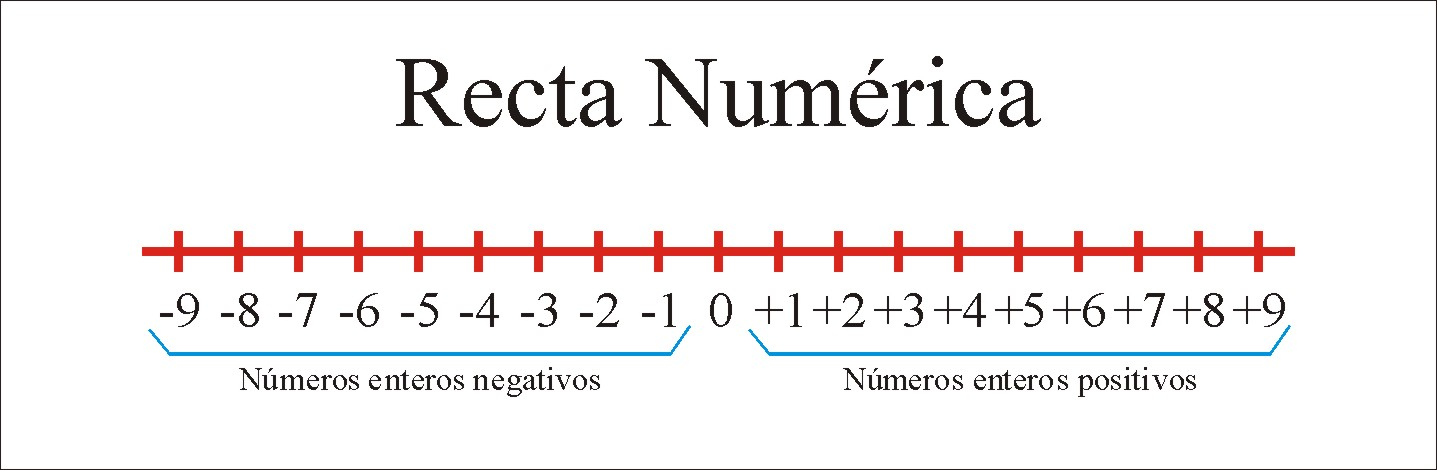
Una recta es una alineación infinita de puntos en la misma dirección. Así bien, la recta numérica es una recta en la que a cada uno de sus puntos le podemos asignar el valor de un número real.
Ahora que ya sabemos qué es, podemos ver con diferentes ejemplos con números naturales, enteros y racionales, cómo ubicarlos en la recta numérica.
Cómo ubicar los diferentes números en la recta numérica
Ubicar números naturales (N) en la recta numérica:
Empezaremos por los más sencillos, los números naturales (N), que son los que utilizamos para contar.
Para empezar, marcamos un punto en la recta al que llamamos 0 y la dividimos en segmentos, todos de la misma longitud. Cada uno representa una unidad, que separa un número entero del siguiente. Así:
Ubicar números enteros (Z) en la recta numérica:
Los números enteros (Z), se representan de la misma forma que los naturales pero también incluyen el sentido contrario a partir del punto al que hemos llamado 0. Así:
Ubicar números racionales (Q) en la recta numérica:
Los siguientes son los números racionales (Q), que incluyen a los enteros y los naturales además de los decimales, son todos aquellos que se pueden expresar en forma de fracción.
Es muy fácil: el denominador de la fracción expresa en cuántas partes iguales tenemos que dividir la unidad y, el numerador, en cuál de esos puntos se localiza el número en la recta.
Por otro lado, si es positivo, se localizará a la derecha del 0 y si es negativo a la izquierda. Así:
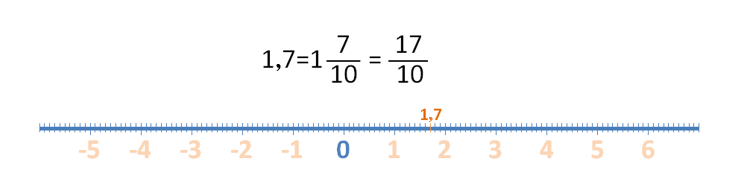
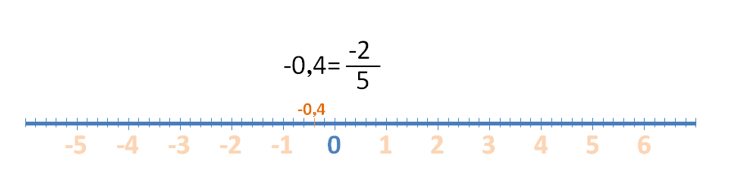
Actividad:

PLANO CARTESIANO
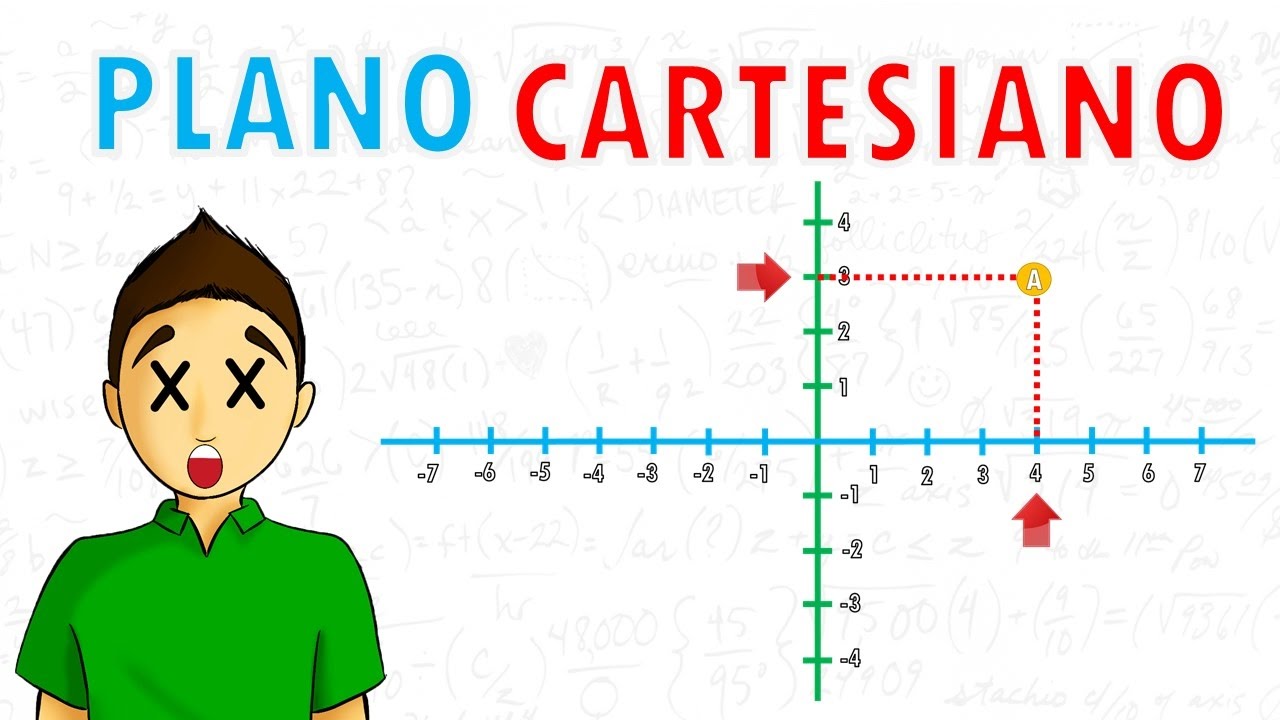
El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto denominado origen. La recta horizontal es llamada eje de las abscisas o de las “x” (equis), y la vertical denominada eje de las ordenadas o de las “y” (yes).
Vas a ver que se forman 4 cuadrados, cada uno de ellos se denominan cuadrantes y se les asigna un número romano, el superior derecho es el primer cuadrante (I) y se numeran en sentido contrario a las manecillas del reloj.

Es muy importante que analices la imagen y no olvides que el primer valor de una coordenada, siempre corresponde al valor de x y el segundo valor es el de y, esto se hace para que cuando veamos una coordenada, no tengamos duda en como ubicarla en el plano cartesiano.
Ahora veamos como localizar una coordenada, veamos unos ejemplos:
Localiza las siguientes coordenadas (2,3), (-3,1) y (-1.5,-2.5)
Para localizar la coordenada (2,3), sabemos que el valor de x = 2, y = 3 ubico en le eje de las x el valor 2 y luego el 3, al cruzarse estos son puntos, ahí encontramos la coordenada, que en este caso esta señalada en color verde.
En la coordenada (-3,1), aplicamos el mismo procedimiento, solo que aquí el valor de x es negativo (-3), así que nos vamos a la izquierda del eje de las abscisas y ubicamos el -3, ubicamos el 1 en el eje de las ordenadas y donde se cruzan ubicamos el punto (-3,1), señalado de color rojo.
Por último, la coordenada (-1.5,-2.5), de igual manera, tenemos que ubicar el -1.5 que se encuentra a la izquierda del eje de las x y el -2.5 que se encuentra abajo en el eje de las y, cruzamos las líneas y ubicamos el punto de color azul.
Gráficamente y de forma más fácil lo podemos ver en el siguiente plano cartesiano.

Por último, aquí tienes más ejemplos, ve como relaciones los números y la coordenada que tienen.

ACTIVIDAD
Realiza en tu cuaderno un plano cartesiano y localiza las siguientes coordenadas:
(+7,+5) (-3,-4) (-1,-6)
(+9,-2) (-5,+8) (0,+2)
(-5,0) (0,0) (+4,-5)
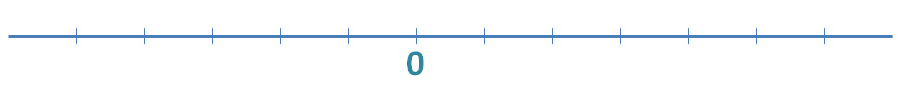
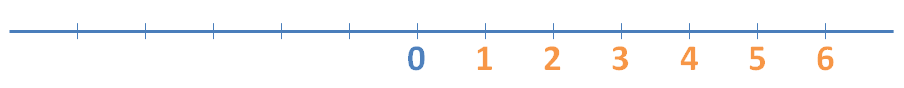
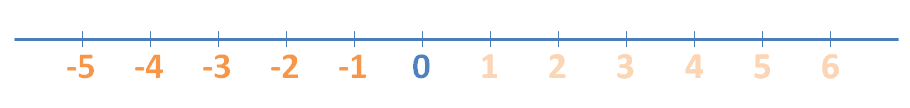
Comentarios
Publicar un comentario