AMPLIFICACIÓN Y SIMPLIFICACIÓN

Amplificar
Es multiplicar el denominador y numerador de una fracción por un mismo número . Esta acción permite que tanto el denominador como el numerador de la fracción aumenten de valor tantas veces como veces se amplifica, pero el valor de la fracción como tal, se mantiene igual. La fracción inicial y su forma amplificada son equivalentes, valen lo mismo..
Por ejemplo, si la fracción se amplifica por dos, significa que el denominador y el numerador aumentarán su valor al doble, pero en este ejemplo y siempre que se amplifique una fracción, se obtendrán fracciones equivalentes; es decir, fracciones que representan la misma cantidad..
Ejemplos:
Fracciones amplificadas por 3.
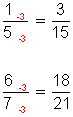
Simplificar
Simplificar una fracción significa dividir por un mismo número tanto el numerador como el denominador, para que la fracción (mostrada ahora con números distintos pero menores) mantenga su proporcionalidad (que su valor se mantenga).
Sólo se podrán simplificar fracciones cuando el numerador y denominador sean divisibles por un número común.
Cada vez que se simplifique una fracción se debe llegar hasta la fracción irreductible , es decir, aquella fracción que no se puede simplificar más (achicar más).
Ejemplos:
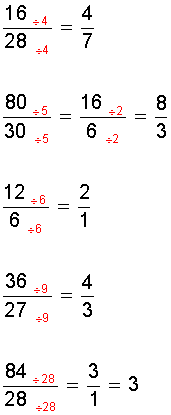
Esta operación, después de ejercitarla y dominarla, normalmente se hace en forma rápida, directa y hasta intuitivamente. Pero para empezar a dominarla debemos considerar los siguientes pasos previos:
Primero
En la simplificación de fracciones, hay que tener en cuenta las reglas de divisibilidad, para saber cuándo un número es divisible por otro.
Reglas básicas de divisibilidad
Regla del 2 . Si un número termina en 0, 2, 4, 6, 8 el número es divisible por 2.
Ejemplos: 42, 58, 12 son todos divisibles por 2 ya que terminan en 2 y en 8
Regla del 3 . Si la suma de los dígitos es un múltiplo de 3, el número será divisible por 3.
Ejemplos: 21 = 2 + 1 = 3 -----> 3 x 7 = 21
27 = 2 + 7 = 9 -----> 3 x 9 = 27
102 = 1 + 0 + 2 = 3 ------> 3 x 34 = 102
48 = 4 + 8 = 12 ------> 3 x 16 = 48
En estos casos, 21, 27, 102 y 48 son múltiplos de 3, así es que el número al que representan es divisible por 3.
Regla del 5 . Si un número termina en 0 ó en 5 es divisible por 5.
Ejemplos: 45, 100 son divisibles por 5 ya que terminan en 5 y en 0.
Segundo
Dominadas las reglas de divisibilidad, debe aprenderse a realizar la factorización prima de un número para factorizar los componentes de la fracción, esto es factorizar tanto el numerador como el denominador de la fracción.
Factorización Prima
Un número es primo si es mayor que 1 y sus factores sólo son 1 y el mismo número.
Ejemplos: 2, 5, 11 son números primos ya que los factores de cada uno son solo el 1 y el mismo número (1 por 2 =2; 1 por 5 = 5; 1 por 11 = 11)
Entonces, tenemos que la factorización prima de un número es el producto de todos los factores primos de un número.
Por ejemplo, hagamos la factorización prima de 12
12
|
2
|
El 12 (divisible por 2, pues termina en 2) lo dividimos por 2 y queda 6
|
6
|
2
|
El 6 (divisible por 2, pues termina en 6) lo dividimos por 2 y queda 3
|
3
|
3
|
El 3 (es número primo, pues es divisible solo por 1 y por 3) lo dividimos por 3
|
1
|
Entonces, tenemos que los factores primos de 12 son 2 . 2 . 3
y vemos que 2 x 2 x 3 = 12
Ejemplo:
Simplificar la fracción:
La factorización prima de 12 es 2 · 2 · 3 y la de 36 es 2 · 2 · 3 · 3
Eliminamos los factores comunes al numerador y al denominador y queda
Ejercicio:
Simplificar 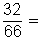
32
|
2
|
.
|
66
|
2
|
16
|
2
|
33
|
3
| |
8
|
2
|
11
|
11
| |
4
|
2
|
1
| ||
2
|
2
| |||
1
|
Hacemos el cuadro como este y vemos que
los factores de 32 son 2 x 2 x 2 x 2 x 2
los factores de 66 son 2 x 3 x 11
Vemos que hay solo un factor 2 que es común, lo eliminamos en ambos lados y queda
Para el numerador 2 x 2 x 2 x 2 = 16
Para el denominador 3 x 11 = 33
Por lo tanto, la fracción 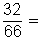
Se convierte, simplificada, en 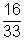
ACTIVIDAD
Dada la siguiente fracción determina dos fracciones equivalentes, a través del método de simplificación:

#2
Encuentra la forma irreductible de la siguiente fracción:

Comentarios
Publicar un comentario